Mēs ar Excel prognozējam, kā aprēķināt variācijas koeficientu

Katru reizi, veicot statistisko analīzi Excel, mums jārisina tādu vērtību aprēķināšana kā izkliede, vidēja līmeņa novirze un, protams, variācijas koeficients. Īpaša uzmanība jāpievērš pēdējam. Ir ļoti svarīgi, lai katrs jaunpienācējs, kurš sāk strādāt tikai ar tabulas redaktoru, varētu ātri aprēķināt vērtību izkliedes relatīvo robežu.

Šajā rakstā mēs jums pateiksim, kā automatizēt aprēķinus, prognozējot datus

Kāds ir variācijas koeficients un kāpēc tā ir nepieciešama?

Tātad, man šķiet, būs lietderīgi veikt nelielu teorētisko ekskursiju un saprast variācijas koeficienta raksturu. Šis indikators ir nepieciešams, lai atspoguļotu datu diapazonu attiecībā pret vidējo vērtību. Citiem vārdiem sakot, tas parāda standarta novirzes attieksmi pret vidējo vērtību. Variācijas koeficientu parasti mēra procentos un ar savu palīdzību tiek parādīta laika rindu vienveidība.

Variācijas koeficients kļūs par neaizstājamu palīgu lietā, kad jums jāveic prognoze saskaņā ar datiem no konkrētā parauga. Šis indikators izceļ galvenās vērtību rindas, kas būs visnoderīgākās turpmākai prognozēšanai, kā arī notīrīs nenozīmīgu faktoru paraugu. Tātad, ja redzat, ka koeficienta vērtība ir 0%, tad ar pārliecību paziņo, ka sērija ir viendabīga, kas nozīmē, ka visas tajā esošās vērtības ir vienādas ar otru. Ja variācijas koeficients pārsniedz vērtību, kas pārsniedz 33%atzīmi, tas liek domāt, ka jums ir darīšana ar neviendabīgu skaitli, kurā individuālās vērtības ievērojami atšķiras no vidējā parauga indikatora.

Kā atrast vidējo kvadrātisko novirzi?

Tā kā mums ir jāizmanto vidējā kvadrātiskā novirze, lai aprēķinātu variācijas indikatoru Excel, būs diezgan lietderīgi uzzināt, kā aprēķināt šo parametru.

No algebras skolas kursa mēs zinām, ka vidējā kvadrātiskā novirze ir kvadrātveida sakne, kas iegūta no izkliedes, tas ir, šis indikators nosaka vispārējā parauga specifiskā indikatora novirzes pakāpi no tā vidējās vērtības. Ar savu palīdzību mēs varam izmērīt pētītā atribūta svārstību absolūto mērījumu un to skaidri interpretēt.

Mēs aprēķinām koeficientu eksolā

Diemžēl Excel nesatur standarta formulu, kas ļautu automātiski aprēķināt variācijas indikatoru. Bet tas nenozīmē, ka jums būs jāveic aprēķini prātā. Veidnes trūkums “formulas līnijā” nekādā veidā neatceļas no Excel spējām, jo ​​jūs varat piespiest programmu veikt nepieciešamo aprēķinu, manuāli izrakstot atbilstošo komandu.

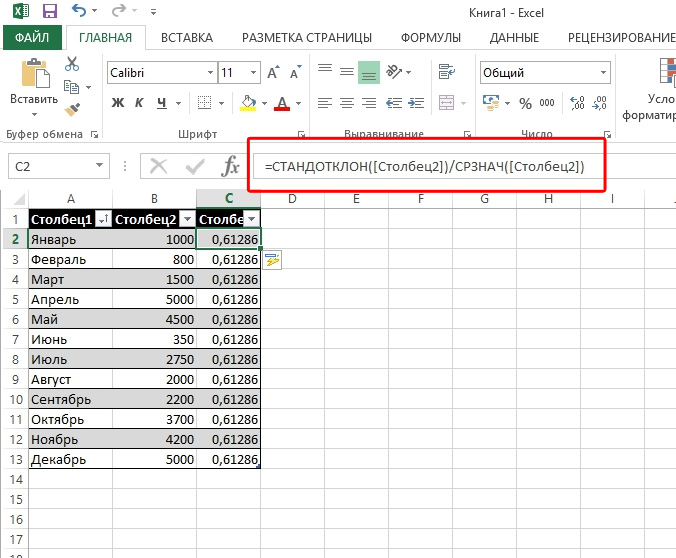
Ievietojiet formulu un norādiet datu diapazonu

Lai aprēķinātu Excel atšķirības, ir jāatgādina matemātikas skolas kurss un sadaliet standartnovirzi vidējā parauga vērtībā. Tas ir, patiesībā formula ir šāda - StandotClon (dotais datu diapazons)/sreble (dotais datu diapazons). Ievadiet šai formulai jābūt tajā šūnā Excel, kurā vēlaties saņemt nepieciešamo aprēķinu.

Neaizmirstiet, ka, tā kā koeficients tiek izteikts procentos, šūna ar formulu būs jāiestata atbilstošajam formātam. To var izdarīt šādi:

1. Atveriet cilni "Sākums".
2. Atrodiet tajā "šūnas formāta" kategoriju un atlasiet nepieciešamo parametru.

Kā opciju jūs varat iestatīt procentuālo formātu šūnā, izmantojot noklikšķināšanu uz labās peles pogas tabulas aktivizētajā šūnā. Parādās konteksta izvēlnē, līdzīgi kā iepriekš minētais algoritms, jums jāizvēlas "šūnu formāta" kategorija un jāiestata nepieciešamā vērtība.

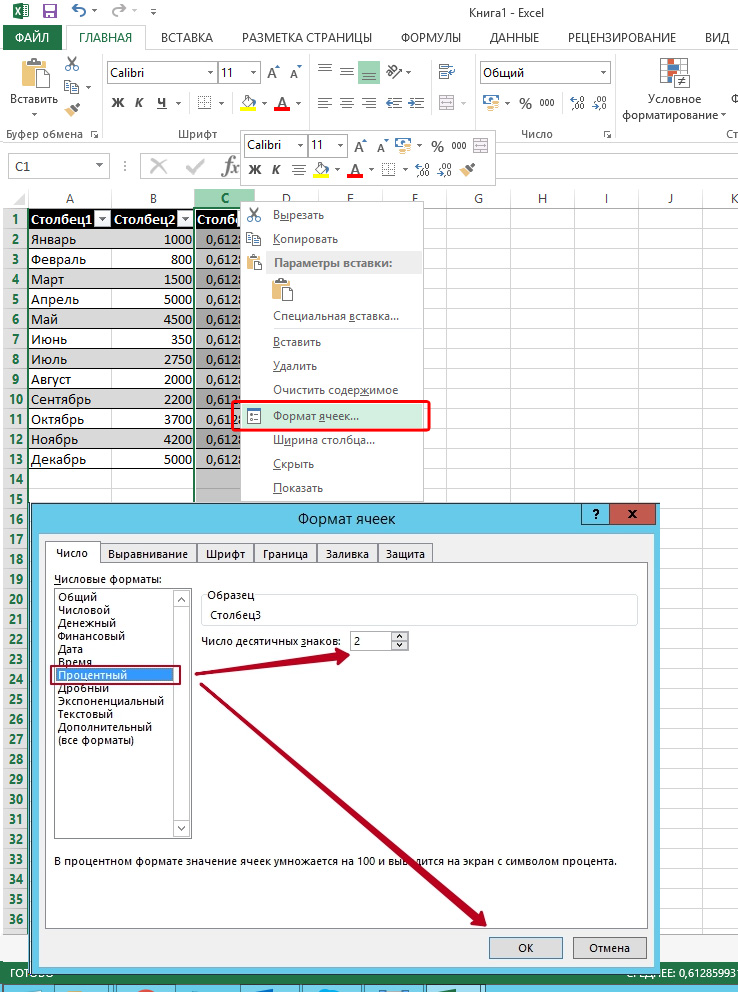
Atlasiet "procentus" un, ja nepieciešams, norādiet decimāldaļu skaitu

Varbūt kāds iepriekš minētais algoritms kādam šķitīs grūti. Faktiski koeficienta aprēķins ir tikpat vienkāršs kā divu dabisko skaitļu pievienošana. Vienu reizi izpildot šo uzdevumu Excel, jūs nekad vairs neatgriezīsities pie piezīmjdatorā nogurdinošiem vārdiskiem risinājumiem.

Jūs joprojām nevarat veikt kvalitatīvu datu izkliedes pakāpes salīdzinājumu? Zaudēts parauga mērogā? Tad šobrīd dodieties uz biznesu un apgūstiet visu teorētisko materiālu praksē, kas tika izklāstīts iepriekš! Ļaujiet prognozes statistiskajai analīzei un attīstībai vairs neliecina par jums bailēm un negatīvismu. Ietaupiet savu spēku un laiku kopā ar planšetdatoru Excel.